月份：2016年10月

MatConvNet是Matlab下用于机器视觉的一个工具包，主要应用是CNN网络，当然其他的网络也涉及到了。MatConvNet简洁、高效，可以用于图片分类、分割和人脸识别等等深度学习的功能。具体的可以参见官网的介绍。

在搭建环境的过程中，发现如今网上对其的资源不太多，所以在这做一个总结。以beta22版本为例。

过程分为下面几个步骤：
1.MatConvNet的下载
2.GPU模式的使用
3.测试

1.MatConvNet的下载

在其官网的页面进行下载，解压到适当的位置。

运行其中“matconvnet-1.0-beta22\examples\vggfaces”路径下的cnn_vgg_faces.m文件，会出现下面的结果，那么说明已经可以使用了。在运行前最好把其中要下载的一些内容给放到对应的文件夹下，这样可以节省一点等待的时间。

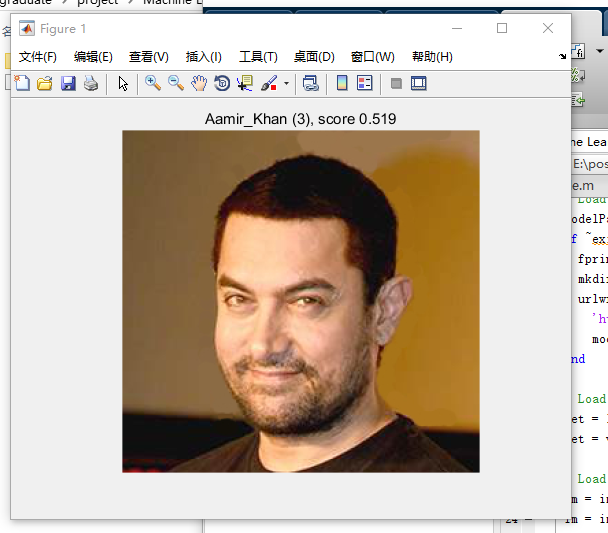
2.GPU模式的使用

官网的这个页面中，提到了搭建GPU的方式。

首先，安装CUDA，在这个页面有下载。记得下载和自己系统以及显卡支持的CUDA。

接下来，要下载cuDNN(The NVIDIA CUDA Deep Neural Network library)。cuDNN是用于GPU加速的一个库函数。在这个页面有下载。

然后把解压好的cuDNN放在合适的文件夹下，建议在MatConvNet下建立local文件夹，同时把cuDNN文件夹中bin文件夹下的cudnn64_5.dll文件复制到matconvnet-1.0-beta22\matlab\mex文件夹下。

最后，在MatConvNet文件夹下建立compileGPU.m文件，其中内容如下。记得把对应的路径给改成自己电脑中的路径。

addpath matlab;

%% with cudnn
vl_compilenn('enableGpu', true, ...
                'cudaRoot', 'C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v8.0', ...  % CUDA的安装路径
                'cudaMethod', 'nvcc', 'enableCudnn', 'true', ...
                'cudnnRoot', 'E:\postgraduate\project\Machine Learning\Deep Learning\CNN\matconvnet-1.0-beta22\local\cudnn');   % cuDNN的路径

出现下面图片中类似的结果，就代表成功了。

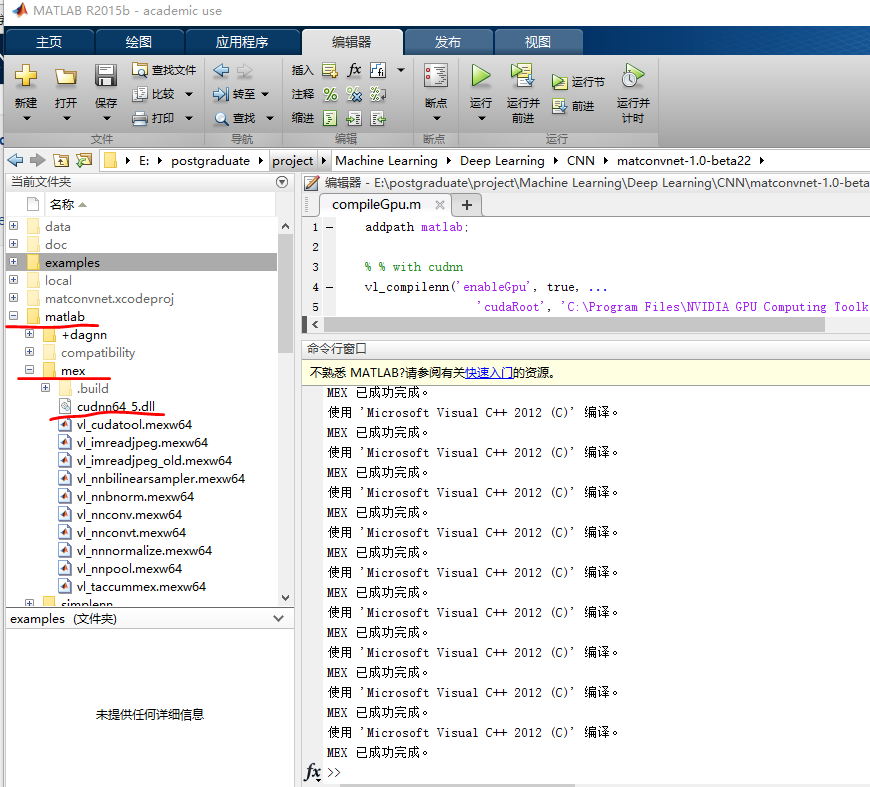
4.测试

还是根据官网的这个页面，在命令行窗口输入vl_testnn命令，测试非GPU模式，会出现下面的内容。

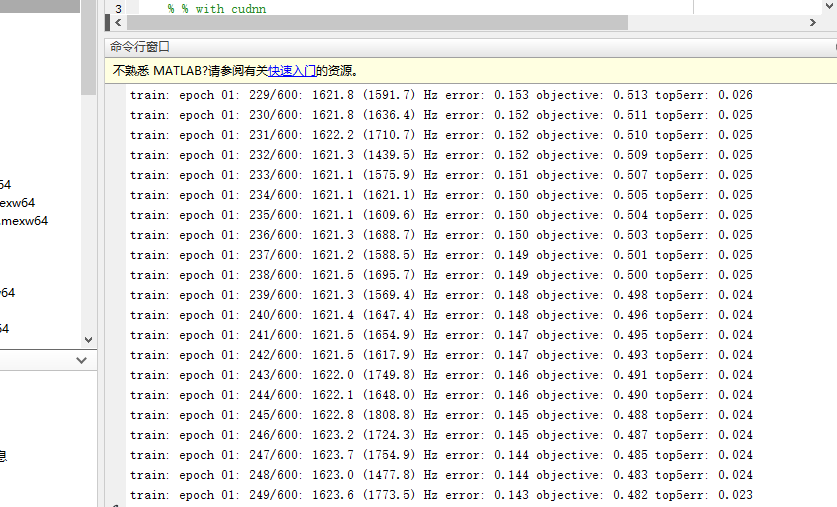
接下来测试GPU模式，在命令行窗口输入vl_testnn('gpu', true)，会有类似上面的内容出现。这就是成功了，GPU模式下的速度提示还是很明显的，一般都会有十倍以上。

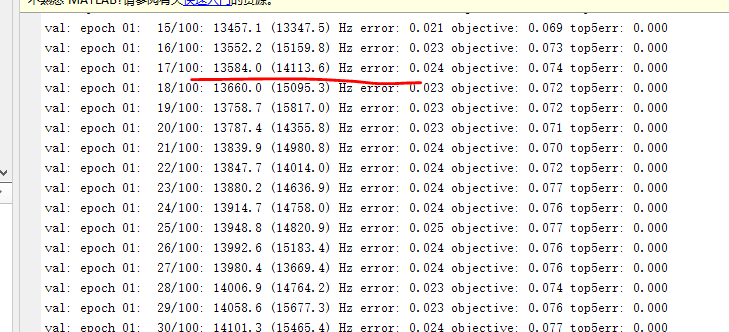
到此，MatConvNet的安装就结束了。

同时，把我在安装过程中遇到的一个问题的解决方式给写一下。在安装cuDNN的时候，可能会遇到如下的错误“Error using mex nvcc fatal : Unsupported gpu architecture 'compute_21'”，其中21可以为其他不能被10整除的数字。这个时候可以把matconvnet-1.0-beta22\matlab下的vl_compilenn.m文件中的732行的代码中"%s"改为向下取10的整数倍。

比如，原代码为

  cudaArch = ...
      sprintf('-gencode=arch=compute_%s,code=\\\"sm_%s,compute_%s\\\" ', ...
              arch_code, arch_code, arch_code) ;

可以改为

  cudaArch = ...
      sprintf('-gencode=arch=compute_20,code=\\\"sm_20,compute_20\\\" ', ... 
              arch_code, arch_code, arch_code) ;

这样，经常遇到的问题就能解决了。

 

动态规划是算法中比较常见的一种分析问题的方式，最近看算法看到这，带着lintcode上面的题目，在这写个总结。

首先从一个lintcode上面简单的题目开始。

Climbing Stairs（爬楼梯）

题目描述：
假设你正在爬楼梯，需要n步你才能到达顶部。但每次你只能爬一步或者两步，你能有多少种不同的方法爬到楼顶部？

样例：
比如n=3，1+1+1=1+2=2+1=3，共有3中不同的方法，所以返回 3。

这是一道非常具有代表性的动态规划的一道问题。

令f[n]记录到达第n阶台阶的方法数。假设你还有最后一步就能到达第n阶台阶，那么最后一步，你可以选择两种方式：1）踏一步以及，2）踏两步。如果是踏一步，那么你要从第n-1阶台阶踏出，此时的方法数是 f[n-1]；如果是踏两步，那么你要从第n-2阶台阶出发，此时的方法数是f[n-2]。所以爬到第n级台阶的方法总数有f[n] = f[n-1] + f[n-2]种。状态转移方程：

f[n] = f[n-1] + f[n-2]

这样可以写出解答的递归形式：

int climbStairs(int n) {
	// write your code here
	if (n <= 1)
		return 1;
	else 
		return climbStairs(n-1) + climbStairs(n-2);
}

此时我们发现可以用一个一维数组来记录之前出现的结果，这样可以省去递归中不必要的空间开销：

int climbStairs(int n) {
	// write your code here
	vector<int> f(n+1);

	f[0] = 1;
	f[1] = 1;

	for (int i = 2; i <= n; i++)
		f[i] = f[i-1] + f[i-2];

	return f[n];
}

其实，这个还可以进一步优化，因为每一步都只需要前两个台阶的结果，所以可以用两个变量来代替一维数组。

int climbStairs(int n) {
	// write your code here
	if (n == 1 || n == 0)
		return 1;
	
	int ways1 = 1;
	int ways2 = 1;
	int ways = 0;
	
	int i = 2;
	while (i <= n)
	{
		ways = ways1 + ways2;
		
		ways1 = ways2;
		ways2 = ways;
		
		i++;
	}
	
	return ways;
}

接下来，我们再来看一题。

Triangle（数字三角形）

题目描述：
给定一个数字三角形，找到从顶部到底部的最小路径和。每一步可以移动到下面一行的相邻数字上。

样例
比如，给出下列数字三角形：

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

从顶到底部的最小路径和为11 ( 2 + 3 + 5 + 1 = 11)。

分析问题，我们发现可以用二维数组来计算到最底层每个位置的最小路径和，令第i层下标为j的位置上最小路径和为f[i][j]。那么，第i层下标为j位置的值f[i][j]，只和i-1层位置j-1下标的最小路径和f[i-1][j-1]以及j位置的最小路径和f[i-1][j]有关。即，f[i][j] = min(f[i-1][j-1],  f[i-1][j])。所以状态转移方程为：

f[i][j] = min(f[i-1][j-1],  f[i-1][j])

同时，发现每次的结果只与上面一层的结果有关，所以省去二维数组，只用一维数组作为辅助。代码为：

int minimumTotal(vector<vector<int> > &triangle) {
	// write your code here
	if (triangle.size() == 0)
		return 0;
		
	vector<int> f(triangle[triangle.size() - 1].size());
	
	// 动态规划过程
	f[0] = triangle[0][0];
	for (int i = 1; i < triangle.size(); i++) 
        { 
                for (int j = triangle.size()-1; j >= 0; j--)
		{
			if (j == 0)
				f[j] = f[j] + triangle[i][j];
			else if (j == triangle[i].size()-1)
				f[j] = f[j-1] + triangle[i][j];
			else
				f[j] = min(f[j-1], f[j]) + triangle[i][j];
		}
	}
	
	// 从辅助数组中找出最小值
	int result;
	result = f[0];
	for (int i = 1; i < f.size(); i++)
		result = min(result, f[i]);
		
	return result;
}

分析这两道题目，发现它们有两个共同的特征：
1.最优子结构：一个问题的最优解包含其子问题的最优解。
2.子问题重叠：一个问题的子问题都是相同的。那么这些子问题可以用同样的方式解决，每次将解决的子问题给记录到表中，在计算之后的问题时查找前面的结果来计算当前问题。这也就是“动态规划”名称的由来了。

在climbing stairs问题中，到达每个位置的方法个数，和之前的所有方法是相关联的。即，到达第n阶台阶的所有的方法个数，同时需要找出第n-1阶台阶的所有的方法以及第n-2阶台阶的所有的方法，以此类推。如果之前的问题找出的不是所有的方法数，那么第n阶台阶找出的结果也不是所有的方法数目。而且，第n阶台阶的求解方式和之前的台阶的求解方式是相同的。

在triangle问题中，每个位置的最小路径和需要知道前一层此位置和下一个位置的最小路径和，如果前一层的结果不是最小路径和，那么此层求出的就不是最小路径和。同样，每层问题的求解方式和之前层问题的求解方式是相同的。

所以，这也就是《算法导论》一书中表述的动态规划的两个特征：
1.最优子结构
2.子问题重叠

参考资料：

1.lintcode
Triangle
Climbing Stairs

2.《算法导论（第三版）》。
第15章动态规划